Seda, et Andy Weiri raamatud mulle meeldivad, olen ma juba pikemat aega kilganud. Ennekõike on see meeldivus seotud veidra nohiklikkusega – tema raamatud on alati põimikud, milles ilukirjandusliku teksti vahele on peidetud hiiglaslik ülesannetekogu. Esmalt antakse lugejale täpselt piisavalt andmeid, et iseseisvalt üle arvutada. Olgu näitena siin koht, kus peategelane jälgis päikeseplekkide kiirust – lugejale anti ette vaadeldava tähe näiv läbimõõt ekraanil ning plekkide näiv liikumiskiirus ekraanil. Eriti nohiklik lugeja (mina) teisendas skaalad, guugeldas meie kodupäikese plekkide liikumist ning jõudis juba terve lehekülje jagu enne raamatu peategelast tõdemuseni, et see, mida too vaatas, ei saanud teps mitte meie kodune Päike olla.
“Ave Maria” üllatas mind aga üsna esimestel lehekülgedel sootuks veidramalt:
„„...Kui palju on kuupjuur kaheksast?”
Hingan sügavalt sisse ja lausun aeglaselt: „Kaks korda e astmel kaks korda i korda pii jagatud kolmega.”
„Vale. Kui palju on kuupjuur kaheksast?”
Aga see ei olnud vale. Ma lihtsalt tahtsin teada, kui tark arvuti on. Vastus: mitte eriti.”
Nonii! Esmapilgul just see, millest rääkisin - imearmas, natuke juhet kokkujooksutav ja natuke intrigeeriv. Loomulikult oli vaja see endal üle arvutada. Pähkel eeldas mõningast (lapse) konspektides surfamist, sest tuleb tunnistada, et viimatisest imaginaararvudega tegelemisest on päris palju aega möödas. Meeles oli vaid hägus teadmine, et kui konspekti näen, suudan välja mõelda, sest see ei saa kuigi keeruline olla. Tulin koju, võtsin paberi ja pastaka ning hakkasin asja kirja panema. Sõnaline lause ei ütle mulle kui paljud asjad sealt tegelikult astendajas on ja mismoodi selle arvu täpne kirjapilt välja näeks. Võib olla nii, naa või kolmandat pidi, näiteks:
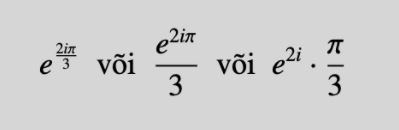
Aga kirja pidi see saama nii, et vastuseks üks tuleks, seega lihtne loogika ütles, et kui „kaks korda e astmel kaks korda i korda pii jagatud kolmega” on kaks, siis „e astmel kaks korda i korda pii jagatud kolmega” peab olema üks... Proovisin, vaatasin, kirjutasin arvu erinevaid variatsioone trigonomeetrilisele kujule välja... No peaaegu, aga mitte päris. Hetkeks tekkis tunne, et mina olen eesel. Võtsin appi lapse ja guugli ja matemaatikute konspekti (muuseas pirisen selle üle, et matemaatika erialal on täna sigahead konspektid – mingid kergemad ained on isegi minu jaoks pelgalt pealevaatamisega loetavad ja hoomatavad, suuremat süvenemist nõudmata)... Ja no ei saa! Lõpuks oli üsna selge, et raamatus on ilmselt viga, aga kui siuke autor laseks oma raamatusse sellise vea sisse, oleks veeb tänaseks juba katki suurest fännide porinast. Noh, on autoreid, kes mängivadki minusuguste peal - anname piisavalt andmeid, et lugeja saaks ise arvutada ja kaasa mängida - kõne all olev on üks neist. Porinat ei leidnud, küll aga leidsin originaaltsitaadi (mille järgi ka mina saan vastuse, et raamatus kirjeldatud pardaarvuti on loll):
“What is the cube root of eight?” the computer asks.
“Where am I?” I say again. This Time it’s easier.
“Incorrect What is the cube root of eight?”
I take a deep breath and speak slowly. “Two times e to the two-i-pi.”
“Incorrect What is the cube root of eight?”
But I wasn’t incorrect. I just wanted to see how smart the computer was. Answer: not very.
Panite tähele? Ingliskeelses esmatrükis puudus kolmega jagamine ja just see kolm ei mahtunud minu arvutusoskusesse. Neile, kes matemaatikaga enam ammu kokku pole puutunud, räägin ära, et kui see raamatus antud imaginaararv geomeetrilisele kujule viia, siis taandub kõik kenasti reaalarvuliseks kaheks. Meeles tuleb pidada vaid põhikoolis õpitud detail, et sin (2π)=0 ja cos(2π)=1 ning siis on ka koheselt ka näha, kuidas i välja taandub ja… :
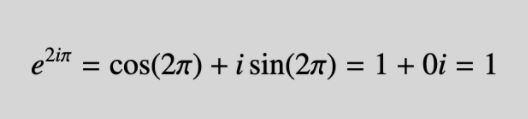
Esmalt tundsin end natuke petetuna. Seejärel vihjas Toomas Krips, et tegelikult on tõlkelahendus ka õige. Nõjatusin tahapoole, vaatasin arve uuesti, kulutasin kaks sekundit mõtlemiseks ning tagusin siis peaga vastu lauda. Juba põhikoolis õpetatakse ju, et jagaja astendajas tähistab juurijat, seega kui „e astmel kaks korda i korda pii” on üks, siis „e astmel kaks korda i korda pii jagatud kolmega” on kuupjuur ühest ning siinkohal sobib see ka, pruukimata olla sealjuures selge reaalarvuline üks.
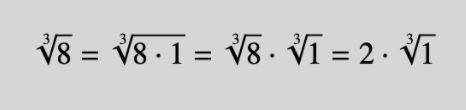
Kui nüüd pilk taas natuke kõrgemale viia, sai juba leitud, et arvu üks võib välja kirjutada kujule „Kaks korda e astmel kaks korda i korda pii” ning sealt edasi siis: „Kaks korda e astmel kaks korda i korda pii jagatud kolmega”...
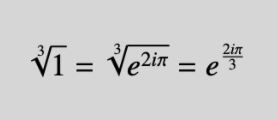
Aga nüüd ei andnud hing rahu! Kuidas on võimalik, et eestikeelseks saamisel oli raamat võibolla targemaks saanud? Kaevusin natuke sügavamalt. Esmatrükis oli ilusasti sees lihtsam variant - selline variant, mille kohaselt võin üheselt väita, et raamatus kasutatav pardaarvuti oli lollim kui lihtne raamatukoguhoidja (siinkõneleja näitel), kuid Penguin Australia kodulehel on juba vastusesse sisse kirjutatud ka kolmega jagamine. Hmm. Seega kuskil Ameerikast Austraaliasse liikumise ajal võis juhtuda, et pardaarvuti sai targemaks. Seda viimast ei saa küll kinnitada, kuid välistada ei saa ka mitte. Võimalik, et ka Austraaliasse jõudes poleks pardaarvuti ka esmase, lihtsama versiooniga leppinud, kuid seal esitas koomast ärkav patsient keerukama vastuse. Pardaarvuti areng seega võis, kuid ei pruukinud toimuda. Peategelase areng toimus üsna kindlasti, kavaluse aste muutus. Teisalt ei saa ma peategelast aga mitte kuidagi „tavalise raamatukoguhoidjaga” võrrelda, sest ma pakun, et ei ole olemas sellist joobe- ega vaimse tervise hetke, mil ma küsimusele “mis on kuupjuur kaheksast?” vastaksin “kaks korda e astmes 2iπ”, kolmega jagamisest rääkimata. Samas, pärast selle artikli kirjutamis? Mine sa tea, ehk kinnistubki.
“Ave Maria” on ka pelgalt ilukirjandusliku teosena üsna geniaalne ja kindlasti lugemist vääriv, kuid lisaks sellele võis tillukesi ülesannetekogule viitavaid nohikumänge leida iga mõne lehekülje tagant. Enamasti olid need sellised gümnaasiumi või ülikooli esimese aasta tasemel arvutustega ehk keskmisele nohikule maksimaalselt guugeldamise kaugusel. Tõsi, eestikeelses variandis on sees veel peotäis lisaülesandeid “otsi üles kohad, kus tõlkija aru ei saanud, mida ta teeb?” (eriti õnnetu näitena siis liikumisvõrrandi teisendamine), kuid tõlkija vähesed reaalteadmised ei takistanud raamatu nautimist. Mõnes kohas küll panid kulmu kergitama ning ilmselt oleks raamatule suuresti kasuks tulnud, kui mõni reaaltaustaga inimene selle enne trükki minemist läbi lugenud oleks, kuid kõik oli hoomatav ning kui mitte otse tõlkest mõistetav, siis kõrval asuvate lausete kaudu teisendatav. Lugesin, mängisin, nautisin. Kuidagi peab ju inimene ka selle ilmaga sooja saama - vähemalt hingele! Väikese optimistliku nügimisena ning läbi arvutama julgustamisena olgu lõppu veel mõte, et kui juba välja arendatud, komade vahele kinnitatud ja trükivärviga paberile pandud raamatukangelane suudab enne järgmise trüki ilmumist targemaks saada, siis lugejal, kes teadusulme raamatus hetketi peatub ning oma käega midagi läbi arvutama asub, on see areng palju kiirem ja kergem tulema.